Writing Linear Equations

Tags

mathematics, slope, slope-intercept form, writing linear equations, y-intercept

Today in class you learned how to write a linear equation using the slope formula and the y-intercept. Reference the following as a review!

The general form to write a linear equation is in slope-intercept form.

Photo credit: https://slideplayer.com/slide/7447234/

The slope formula is: 

To use this formula you take two given points and plug them into the equation.

For Example:

Find the slope of the points (0, 8) and (2, 12).

Label (0, 8) as (x₁, y₁) & (2, 12) as (x₂, y₂)

 

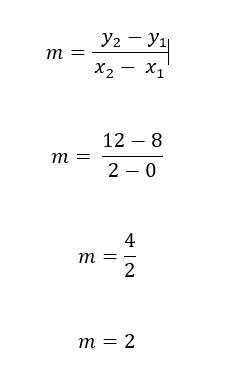
Now that you have your slope as 2, you need to find the y-intercept in order to write a your linear equation.

**Remember that the y-intercept is the point where the line crosses the x-axis. **

For Example look at the following graph. You can see that the where the line crosses the y-axis is your y-intercept.

Photo Credit: http://www.mathwarehouse.com

 

What is the x-coordinate at that point?

If you guessed 0, you are correct! 

** The x-coordinate for any y-intercept will always be 0! **

Now if we refer back to our two original points, they were (0, 8) and (2, 12).

Knowing that in the coordinate (0, 8) the x-coordinate is 0, therefore our y-intercept must be 8.

So now, we know our slope is 2 and our y-intercept is 8. Our last step is to plug it into slope-intercept form.

y = mx + b

m = 2 and b = 8

y = 2x + 8

There are times where one of the points won’t contain the y-intercept. In order to find the y-intercept you must plug the one of the points and the slope into y = mx + b in order to solve for b. 

Directions for Assignment:

1. Watch the following  video from Khan Academy to see more problems on how to solve for the y-intercept of an equation given any two points. 
2. If you would like to practice some problems before taking your HW Practice Assessment, click “Practice: Slope-Intercept from two points” which is located on the left side of the screen next to the video. If you can’t locate it, click this link.
3. After you have watched the video and solved some practice problems, click on the following link and solve the problems! We will review the problems and responses in class tomorrow!

If you have any problems or concerns, please email me at ccolechn@buffalo.edu