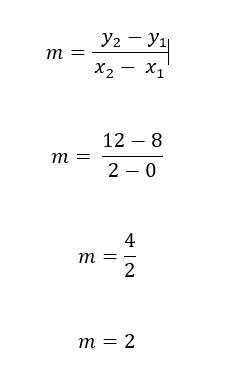Introduction:
In the article, “Developments towards Mathematical Citizen Science”, Anna M. Hartkopf mentions a theory by Matt Parker on a three-sided coin. He posted to Twitter asking for help on determining the thickness of a coin so that the coin would land on its edge ⅓ of the time. He created his own website in which he provides a video introduction of determining the thickness of a coin, how to make various three-sided coins, and how to test those out to determine if it will land on its edge ⅓ of the time. For this project, you will watch the video provided, create various three-sided coins, use mathematics to determine surface area and thickness, and test your coins through trial and error to determine if they can create a coin that will land on its edge ⅓ of the time, and determine what that thickness must be.
Objective:
To investigate Matt Parker’s question: How thick is a three-sided coin? You will create various three-sided coins with different thicknesses and determine if any of their coins land on its edge ⅓ of the time.
Materials:
- Math Binder
- Pencil and pens
- SmartBoard
- Quarter, Nickel, Dime, Penny
- Cups
- Internet Access to the following:
- Worksheets printed from Think Maths Webpage
- Various three-sided coins from:
- Paper Towel Dowels
- Toilet Paper Dowels
- Cylinders (food cans)
- Broom handles
Step 1: Engage
The lesson will begin by asking you to think if it is possible to create a three-sided coin would be able to land on “heads”, “tails”, and its “edge”, equally ⅓ of the time. You will look at a quarter, nickel, dime, and penny to observe and use what you know and create your own hypothesis to determine your answer. You will write whether or not they you think there is a three-sided coin that would be able to land on each surface ⅓ of the time, along with an explanation. After, you will discuss your hypothesis and share their thoughts aloud. I will then show you the Three-Sided Coin Introduction Video, to introduce you to the lesson. Afterwards, you will discuss what you saw in the video, and if your hypothesis changed thus far. You will then be broken into groups of 4-5 people, in which you will investigate this topic even more.
Step 2: Explore
You will begin your study by first answering the questions below. These are the worksheets provided by Matt Parker on Think Math’s webpage.
You will then answer the questions:
- How could we estimate experimentally the probability that a particular coin lands its edge?
- How might we make a coin of a given thickness?
- What would need to be true of the material making up the inside of the coin, in order to make the probabilities depend only on the thickness of the coin?
- What else might affect the probability? If you want to compare across throws, how can you make sure your test is fair?
After answering these questions, you will move onto Method 1, in which you look at the coin and the sphere.
A formula you might find useful:
The Surface Area (SA) of the shaded region is: 2πrt
1) Write down the surface area(SA) of the sphere in terms of r:
2) Given the SA of the shaded region is one third of that of the sphere, Write r in terms of t:
3) Consider the right angled triangle and write a formula that connects h,t and r:
4) Can you use these last two results to find the ratio between h and t?
After exploring the coin and sphere, you will move onto Method 2, which is the coin and the circle.
1) Find the angle x, given that the two dashed arcs make up one third of the circumference:
2) Find the angle y.
3) Use right-angled triangle trigonometry, and the angle y, to find the ratio between h and t.
After you conduct the two methods, you will then create your own three-sided coins. Each group will create 3 different three-sided coins, each made from different materials. you will label with a pen, H on one flat side and T on the other flat side. You will use the following chart to toss their coins and record your answers. You will use one sheet for each coin, totaling three data sheets.
After you have investigated your three-sided coins, you will use GeoGebra to create a bar graph for each of your three-sided coins, with the number of times it landed on heads, tails, and the edge. You will then look at Jen Rogers’ calculations to determine if your results are statistically significant.
After you review Jen’s work, you will determine if your coins are statistically significant or not. You will write down why or why not and use evidence to support your answers. You will then input your work into the Google Form Submission, the Matt Parker set-up on Think Math’s webpage. You will then go back to your original hypothesis and determine if you were correct when you stated whether or not there could be a three-sided coin in which it would land equally on ⅓ on each of the faces and the edge.
Step 4: Social Media
After you have collected and analyzed their data, you will post on Social Media. You will start by creating your own Twitter Group account and reply to Matt Parker’s original tweet with your findings, as well as your own thoughts. You are encouraged to use hashtags, as well as view other people’s posts on the twitter thread. In addition, you will reply to this blog post with in a comment under my blog with your findings and data analysis.
If you have any questions, please contact me at ccolechn@buffalo.edu.
Have fun! 🙂